Entangling single atoms over 33 km telecom fibre
07.07.2022
Quantum networks facilitate the distribution of entanglement between distant quantum memories, thereby offering a modular approach to quantum computing and providing the entanglement required for secure quantum key distribution protocols. Photons are the ideal candidate to mediate the distribution process due to their non-interactive nature and physical channels can be realised using the already existing optical fibre infrastructure. Most quantum systems under active research, however, do not operate in the low loss telecom regime – limiting fibre link lengths to a few kilometres due to attenuation losses in the fibre.
We recently observed heralded entanglement between two rubidium atoms generated over telecom fibres with a length up to 33 km. For this, we worked together with Matthias Bock and Christoph Becher from the University of Saarland, who developed efficient, low-noise, and polarization-preserving quantum frequency conversion devices. The devices efficiently interface our atomic quantum memories that operate at 780 nm to telecom wavelength and hence significantly reduce optical attenuation losses in long optical fibres.

Picture of the experimental setup in Lab 1 to trap and manipulate a single rubidium atom. © Jan Greune.
The entanglement fidelity between the atoms was analysed for different fibre lengths, as shown in blue in the figure below. Decoherence of the atomic quantum memories limits the fidelity for long fibre links. Our next goal is to improve the memory storage time in both nodes to increase the atom-atom entanglement fidelity for long fibre links.
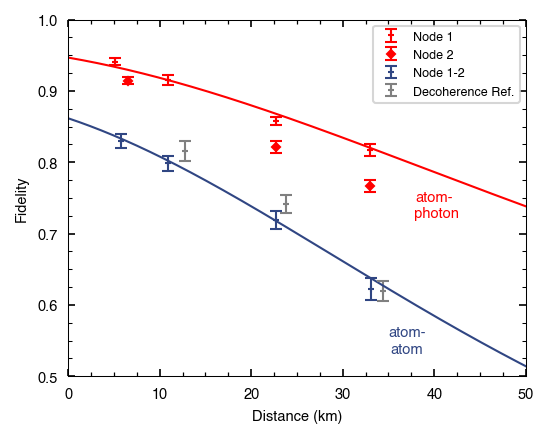
Observation of atom-atom (blue) and atom-photon (red) entanglement generated over long telecom fibre links. The solid lines are simulation results based on a decoherence model of the atomic quantum memories together with photon attenuation losses in the long optical fibres. The expected atom-atom entanglement contrast equals the product of the atom-photon contrasts of Node 1 and 2 multiplied by the two-photon interference contrast (~0.95).

