Systematic errors in current quantum state tomography tools

Quantum state tomography is the standard tool to determine the density matrix of an experimentally prepared quantum state. In order to guarantee physicality of the result, one normally resorts to reconstruction algorithms based on maximum likelihood or on least squares optimization. However, as shown in this work, these methods suffer from a systematic underestimation of the fidelity and an overestimation of entanglement. In contrast, a linear evaluation of the data allows avoiding such strongly biased estimates.

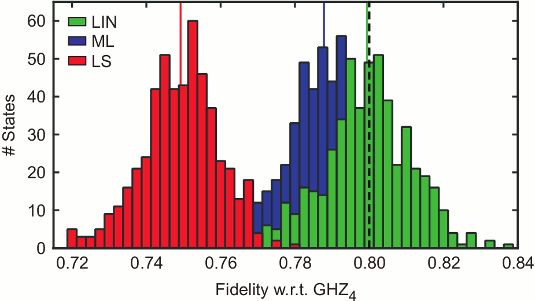
Histogram of the fidelity estimates of 500 independent simulations of quantum state tomography of a four-party GHZ state mixed with white noise for three different reconstruction schemes. The results obtained via maximum likelihood (ML, blue) or least squares (LS, red) fluctuate around a value that is lower than the initial fidelity of 80% (dashed line). For comparison, we also show the result using a linear evaluation of the data (LIN, green), which does not have this systematic error called bias.